Out of equilibrium dynamics
One of the most interesting open questions is about the out of equilibrium dynamics: how does closed quantum systems reach a stationary state (if any)? What is the nature of the transient states?
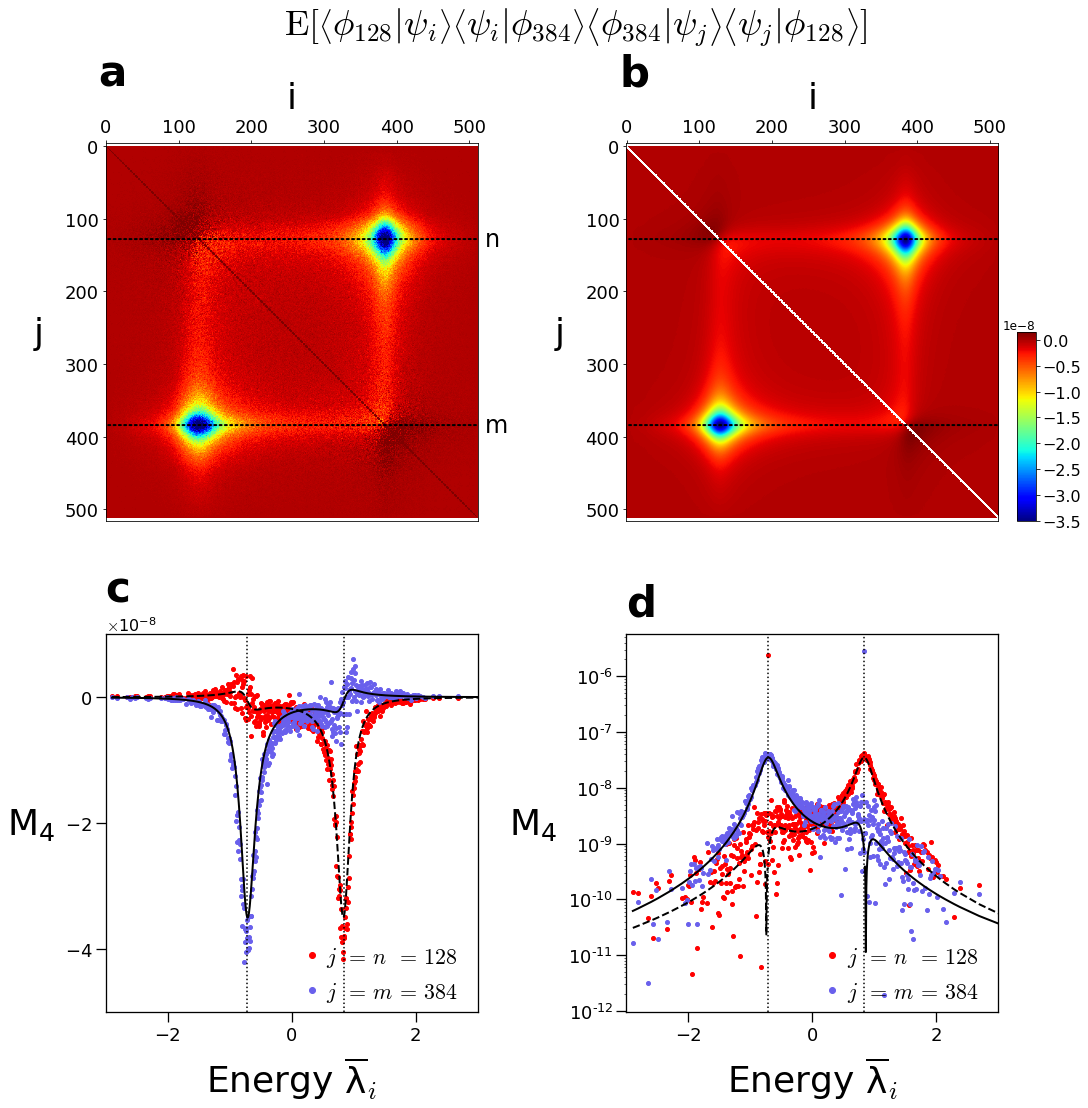
Within our framework, if an ensemble of random interaction Hamiltonians exhibits dynamical typicality, it is then in principle possible to obtain the state of any subsystem at all times by averaging over the randomness. Such calculation requires the spectral and eigenvector statistics of order 2 and 4 respectively for the specific class considered. These quantities can be obtained from the average of the Green functions and their covariance. We developed a new technique for calculating these quantities[1] and more generally the mixed moments of Green functions for random biased Hamiltonians, i.e. of the form \(\hat{H}=\hat{H}_0+\hat{W}\) where \(\hat{H}_0\) is diagonal deterministic and \(\hat{W}\) is random. This technique has the main advantages of being simple, non perturbative, and most importantly, versatile: it can be applied to various statistics of the additive random term \(\hat{W}\) (see Fig. for the Gaussian interaction case).