Unconventional Stationary States
The question of whether a quantum system can converge towards a stationary state different from the usual thermal one has received much attention recently through breakthrough experiments with cold atoms in optical lattices and trapped ions, putting into evidence several mechanism to prevent conventional thermalization, e.g. around an integrability point or with a Many Body localization phase transition.
On the theoretical side, we proposed recently a random matrix model which provides some results. Assuming a given class of random interactions verifies the property the quantum dynamics is typical, then the reduced density matrix of any subsystem can be obtained in principle by averaging over the randomness. We performed this averaging for several classes of random interactions and demonstrated the existence of unconventional stationary states involving a new partition function of purely quantum origin. This partition function recovers the Boltzmann distribution as a particular case (see [1]).
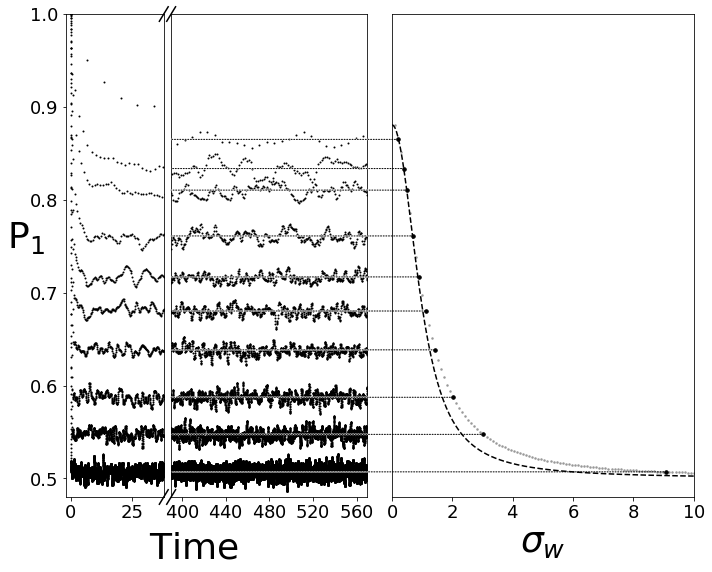
Interestingly, this new partition function allows to capture a crossover between a microcanonical ensemble defined locally in energy (i.e equiprobability of the accessible states in a tiny energy window around the initial energy of the system) and a micro canonical ensemble defined globally in energy (i.e. all states are accessible and equiprobable) as shown on the figure below.
The statistical physics we obtain within this framework can be considered as unconventional for the two following reasons. First, our starting hypothesis is to put randomness in the nature of the system (here the interaction between its subparts) in the spirit of Wigner and Dyson use of random matrices, however with a notable sophistication: the randomness is only in the interactions and the system's subparts Hamiltonians can be chosen arbitrarily. This is to be contrasted to the standard approach of statistical physics where randomness is introduced on the state of the system (c.f. microcanonical ensemble). Second, the analytical results we obtained demonstrate unconventional stationary states, i.e. coming from a new thermodynamical ensemble more general than the microcanonical one.