Typicality of quantum dynamics
To tackle the many body quantum problem in the most general way possible, we start by making an assumption which might seem at first sight unrealistic. We consider a composite quantum system (chosen arbitrarily, e.g. a set of identical particles) and we assume the interactions between the subparts of the system to be random. This indeed goes against the intuition that physical Hamiltonians should a priori be modeled using fully deterministic operators (e.g. Hubbard or Ising Hamiltonians).
However, introducing such randomness can prove to be very fruitful on various aspects in particular in terms of analytical capabilities. This was Wigner's original idea when considering the atomic nucleus Hamiltonian like a random matrix [1]. Proceeding this way, he made a crucial departure from the usual statistical physics approach where randomness is introduced on the state of a system. This step moved towards a new statistical physics where randomness is now introduced into the nature of the system itself, i.e. its Hamiltonian. This radical change of point of view was originally justified on heuristic grounds: in practice, physically relevant quantities, i.e. accessible by experiments, do not depend much on the details of the realization of the disorder associated to the randomness. These physical observables seem to take typical values dependent only on some conditions constraining randomness and summarizing its macroscopic properties, e.g., symmetry class: hermitian or real symmetric, spectral variance, the possibility of a block diagonal structure due to selection rules.
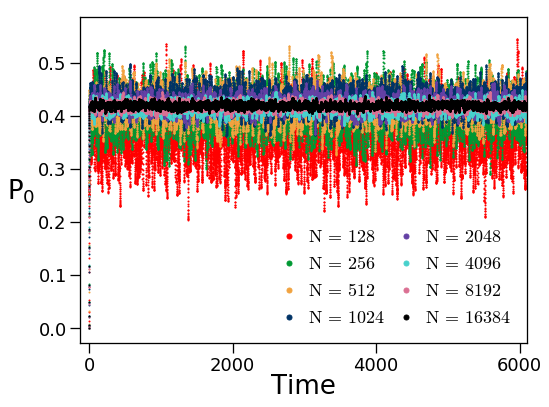
Very recently, we provided a rigorous ground for justifying this approach, with a notable sophistication compared to Wigner’s framework: we can chose arbitrarily the subparts Hamiltonians keeping the randomness in the interaction Hamiltonian only. We considered an arbitrary quantum system \(S\) coupled non perturbatively to an arbitrary quantum environment \(E\) and introduced some randomness in the interaction. Then, we proved that, when the dimension of the Hilbert space of the environment becomes large, the system \(S\) follows a "typical" dynamics (see Fig.1 and [2]). In other words, the reduced density matrix of \(S\) (which provides the state of \(S\)) does not depend much on the details of the random interaction, it is self-averaging. We demonstrated this property for several classes of random interaction (see also [3,4] for the particular cases of two and four level systems). Conceptually, we think this is a very important result for the following reasons. First, this property can explain the lack of sensitivity to microscopic details of certain quantum processes, e.g. thermalisation. Second, numerical simulations using a single realization of the random interaction provide, in one run, the typical dynamics. Finally, probably the most important consequence of this property is that it provides a non perturbative analytical method for calculating an approximation of the reduced density matrix of S (i.e. the state) simply by averaging over the interaction, all other parameters being fixed and arbitrarily chosen: initial state, Hamiltonians of the system \(\hat{H}_s\) and the environment \(\hat{H}_e\). These results rely on a generalized central limit theorem called "measure concentration" (see Mathematical tools). We applied this calculation technique to get the stationary states of an embedded quantum system (see Unconventional Stationary States).